Aufbauend auf meinen Beitrag über die Berechnung von RR-Intervallen und Herzschlagrate möchte ich die Berechnung des Poincaré-Diagramms für HRV-Interessierte nachvollziehbar machen, die weniger technische Vorbildung mitbringen (zu denen ich auch gehöre).
Das nach dem Mathematiker Henri Poincaré benannte Diagramm ist ganz allgemein betrachtet ein Hilfsmittel, um Dynamik und Selbstähnlichkeit in Phänomenen zu erkennen. Auch Bezeichnungen wie z. B. Poincaré-Plot, Lorenz-Plot, Phasenraumdiagramm, Streudiagramm oder Recurrence-Plot werden verwendet. Sie bedeuten aber im jeweiligen Zusammenhang nicht unbedingt dasselbe. Das Poincaré-Diagramm wird seit 1991 (siehe Raetz SL, Richard CA, Garfinkel A, Harper RM. Fundamental Research Dynamic Characteristics of Cardiac RR Intervals. Sleep. 1991;14(6):526-33) auch zur Beschreibung der Herzratenvariabilität (HRV) verwendet.
Im Prinzip einfach
Die Idee, wie das Poincaré-Diagramm in seiner zweidimensionalen Form (ja, mehrdimensional ginge auch) bei der HRV-Analyse verwendet wird, ist genial einfach:
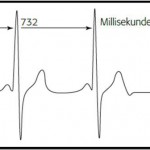
- Es werden immer zwei aufeinander folgende RR-Intervalle einander zugeordnet und ins Diagramm eingetragen. Das heißt, dass der Wert eines RR-Intervalls (RRn) auf der x-Achse und der Wert des nächsten RR-Intervalls (RRn+1) auf der y-Achse gesucht werden und dementsprechend ein Punkt ins Diagramm eingetragen wird.
- Dann wird in der Reihe der RR-Intervalle um ein RR-Intervall weitergegangen und derselbe Vorgang wiederholt, bis alle RR-Intervalle eingetragen sind. Mathematiker formulieren das gerne so: Jedes RR-Intervall wird als Funktion des jeweils vorherigen RR-Intervalls dargestellt.
Um den Aufbau des Diagramms zu veranschaulichen, soll der geschilderte Vorgang im folgenden Schaubild verdeutlicht werden. Die RR-Intervall-Paare dienen als Koordinaten im Diagramm. Die Nummerierung der RR-Intervall-Paare soll helfen, die zeitliche Reihenfolge der RR-Intervalle besser nachvollziehen zu können. Um die Übersicht zu behalten, wird zunächst nur ein Zeit-Ausschnitt von 5 Prozent einer 5 Minuten langen EKG-Messung dargestellt.
Das Aussehen beurteilen
Die Form der Punktwolke kann visuell-qualitativ für die Beurteilung der HRV verwendet werden. Dabei werden verschiedene Formen wie z. B. “Zigarre”, “Torpedo”, “Flügel”, “Galaxis”, “Komet” oder “kleine runde Scheibe” unterschieden und auf Basis von Studien physiologischen Zuständen zugeordnet.
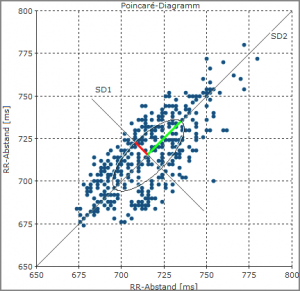
Ein typisches Poincaré-Diagramm einer gesunden Person ist eine gedehnte, elliptische Punktwolke.
- Schlägt das Herz während der Messung fast immer mit der gleichen Pulsrate und mit geringer Variabilität, dann ergibt sich eher eine kleine Scheibe.
- Ändert sich der Herzschlag gleichmäßig während der Messung innerhalb eines gewissen Bereichs (z. B. zwischen 60 und 80 Schlägen pro Minute) und besteht eine in etwa gleichbleibende Variabilität, dann kann das zu einer als normal geltenden Flügelform führen.
- Je nach Zusammentreffen von anderen Herzschlagcharakteristiken bilden sich andere Formen des Poincaré-Diagramms aus.
- Ungewöhnliche RR-Intervalle, die auf Messfehler oder evtl. Herzfehler beruhen, sind gut zu erkennen, weil sie als “Ausreißer” auffallen.
- Für diagnostische Rückschlüsse ist viel therapeutische Erfahrung notwendig. In meinem Beitrag über die Reaktionsfähigkeit des VNS wird ebenfalls darauf eingegangen.
Die Analyse und Kategorisierung des Aussehens der Poincaré-Diagramme oder des Lorenz-Plots war und ist immer wieder Bestandteil von Forschungsarbeiten. Nach meiner Erfahrung gibt es deswegen viel weiterführende Literatur.
Gerade die schnell erfassbare und leicht unterscheidbare Ausprägung des Poincaré-Diagramms macht es zu einem nützlichen Werkzeug im klinischen Alltag der Kardiologen.
Quantitative Auswertung – Berechnung von SD1 und SD2
Um eine quantitative Auswertung der Punktwolke durchzuführen, wird als häufigste Methode im Wesentlichen die Standardabweichung der Abstände vom Mittelpunkt der Wolke berechnet, jeweils in Richtung der Diagonalen.
Die Gesamtvariabilität kann als Summe dieser zwei Komponenten (SD1 und SD2) verstanden werden. Der Effekt der kurzzeitigen Variabilität wird von SD1 dargestellt, während die Langzeitvariabilität in SD2 steckt. Das bedeutet, dass sich eine allmähliche Änderung des Ruhepulses im SD2-Wert zeigt. Schnelle Änderungen werden im SD1-Wert erkennbar.
Die ermittelten Kennwerte drücken ähnliches wie die HRV-Werte anderer Analysetechniken aus:
- Es ist anschaulich nachvollziehbar (ohne hier selbst den mathematischen Beweis anzuführen, siehe “Reminder: RMSSD and SD1 are Identical Heart Rate Variability Metrics“), dass SD1 und RMSSD dasselbe Phänomen ausdrücken.
- Auch zwischen SD1 und dem HF-Wert besteht ein enger Zusammenhang.
- Zudem ist eine Korrelation des Verhältnisses von SD1 zu SD2 (SD1/SD2) mit dem Quotienten der HRV-Parameter LF/HF feststellbar.
Es gibt sehr viel Literatur über das Poincaré-Diagramm beziehungsweise über seine Verwendung. Im Folgenden möchte ich nur ein paar Beispiele aufführen:
- “A Mini-Review, Albert C.-C. Yang, MD”
- “Do Existing Measures of Poincaré Plot Geometry Reflect Nonlinear Features of Heart Rate Variability”
- “Poincaré plot indexes of heart rate variability detect dynamic autonomic modulation during general anesthesia induction”
Ich hoffe, meine Erläuterung des Poincarè-Diagramms ermöglicht auch HRV-Interessierte mit weniger technischer Vorbildung, eine Vorstellung der Zusammenhänge zu entwickeln.
Die Berechnung der wichtigsten HRV-Werte in ähnlich nachvollziehbarer Weise darzustellen, habe ich mir für die Zukunft vorgenommen.
P. S.: Die Beispieldaten wurden mit einem HRV-Scanner (Modell: Professional) des Herstellers BioSign gemessen, exportiert und mit Hilfe der Programmiersprache R von Erich Langenbuch aufbereitet.