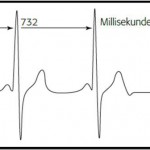
Aufbauend auf meinen Beitrag über die Berechnung von RR-Intervallen und Herzschlagrate möchte ich die Berechnung des SDNN für HRV-Interessierte nachvollziehbar machen, die weniger technische Vorbildung mitbringen (zu denen ich auch gehöre).
Die Berechnung
Die Berechnung des SDNN-Wertes durchläuft folgende Schritte:
- Die aus den R-Zacken des EKG-Signals berechneten RR-Intervalle werden verwendet, um die mittlere Dauer der RR-Intervalle (
- Die Abweichungen der einzelnen RR-Intervalle (
In wissenschaftlichen Veröffentlichungen wird die SDNN-Berechnung üblicherweise komprimierter ausgedrückt:
Standardabweichung (oder Quadratwurzel der Varianz) aller gemessenen RR-Intervalle
Das entspricht der übersetzten Definition, die von der Task Force of The European Society of Cardiology and The North American Society of Pacing and Electrophysiology (ESC/NASPE) 1996 veröffentlicht wurde: “Standard deviation of all NN intervals”. Als NN-Intervalle werden Normal-to-Normal-Intervalle verstanden, die von Artifakten (wie z. B. ektopische Herzschläge) bereinigt wurden. Dies entspricht in der Praxis den messtechnisch aufbereiteten Interbeat- bzw. Beat-to-Beat-Intervallen oder eben auch den RR-Intervallen. Der Vollständigkeit halber sollen hier die mathematischen Formeln nicht fehlen und führe ich sie auch an:
Als alternative Abkürzung zu SDNN findet man gelegentlich RRSD, SD oder SDRR. Allerdings können feine Unterschiede dahinter stecken, wie z. B. bei SDRR die Berücksichtigung aller RR-Intervalle (also ohne Bereinigung von Artifakten und abnormalen Herzschlägen).
Verwendbarkeit und Nutzen
Die SDNN stellt ein Maß für die Gesamtvariabilität im gemessenen Zeitraum dar. Der SDNN-Wert ermöglicht, die von physiologischen Vorgängen verursachten Veränderungen der RR-Intervalle quantitativ zu vergleichen.
Obwohl die SDNN ein einfacher statistischer Kennwert ist, muss man trotzdem auf eine korrekte Anwendung achten. Eine Schwierigkeit liegt darin, dass in die SDNN alle Schwankungen der Herzrate im gemessenen Zeitraum eingehen. Je länger man misst, desto mehr niederfrequente (also langsame) Schwankungen werden mitberücksichtigt.
Der SDNN-Wert ist folglich von der Mess-Dauer abhängig. Je länger sie ist, desto eher fällt der SDNN-Wert höher aus als bei einer Kurzzeit-Messung.
Aus 24-Stunden-Aufnahmen des Herzschlags ergibt sich eine SDNN, die stark mit den HRV-Parametern Total-Power (TP), Low-Frequency (LF) und Ultra-Low-Frequency (ULF, Herzratenschwankungen mit einer Dauer größer als 5,6 Minuten) korreliert (Umetani et al., 1998). Bei 5-Minuten-Messungen hängen die Pulsschwankungen hauptsächlich mit der parasympathisch herbeigeführten RSA zusammen, insbesondere bei langsamer Atemführung.
Bei Langzeitmessungen kommt mit der SDNN also nicht nur zum Ausdruck, wie sich der Parasympathikus entsprechend aktiv in die Einflüsse von Sinusknoten und Sympathikus einmischt. Zusätzlich fließen weitere Regelungsvorgänge ein, wie z. B. Blutdruck- und Wärme-Stabilisation, Tagesrhythmus und Arbeitsbelastung. Damit ähnelt die SDNN den HRV-Werten SD2 oder Total-Power (TP). Statistiker drücken dies dadurch aus, dass sie von einer hohen Korrelation dieser Werte sprechen.
Üblicherweise wird die SDNN in wissenschaftlichen Studien aus 24-Stunden-Messungen errechnet und verglichen. Aber die SDNN-Werte können nicht nur aus Langzeitmessungen, sondern auch aus standardisierten Kurzzeitmessungen verglichen werden. Man muss eben mit Hilfe standardisierter Messbedingungen und Messdauern darauf achten, dass nicht “Äpfel mit Birnen” verglichen werden. Für Vergleiche der Kurzzeit-Variabilität wäre auch der RMSSD-Wert gut geeignet.
Bei Herzinfarktpatienten wurde festgestellt, dass niedere (alters-korrigierte) SDNN-Werte auf eine höhere Erkrankungs- und Sterbewahrscheinlichkeit hinweisen, während höhere SDNN-Werte für höhere Überlebenschancen sprechen. Beispielsweise haben Herzinfarktpatienten mit mittelmäßigen SDNN-Werte zwischen 50 und 100 ms (aus 24-Stunden-Messungen) eine um 400 Prozent geringere Sterberate als Patienten mit SDNN-Werten kleiner als 50 ms. (Kleiger et al., 1987).
Normale Werte
Die SDNN wird sowohl bei HRV-Kurzzeit-Messungen als auch bei Langzeitmessungen (z. B. 24-Stunden-Messungen) berechnet. Für Langzeitmessungen hat die oben erwähnte Task Force der ESC/NASPE von 1996 “Normwerte” der HRV (Mittelwert ± Standardabweichung) empfohlen: für die SDNN 141±39 ms. Solche Normwerte sind allerdings wenig sinnvoll, wenn man die Abhängigkeit der HRV vom Geschlecht und vom Alter nicht berücksichtigt.
Obwohl es aus Studien Richtwerte für normale SDNN-Werte gibt, werden sie oft angezweifelt. Gerade bei älteren Menschen können die Studien ihre Schwächen haben: Meistens sind zu wenig Probanden je Altersklasse beiderlei Geschlechts beteiligt und Vorerkrankungen machen die Einteilung in vergleichbare Gruppen zunehmend komplizierter.
Im Vorsorge- und Fitness-Bereich wird daher nicht der sogenannte Quervergleich zwischen unterschiedlichen Menschen bevorzugt, sondern der “Längsvergleich” von HRV-Werten einzelner Personen. Es werden Veränderungen der SDNN (und des RMSSD) aus vielen Messungen der jeweiligen Person gewonnen und persönliche Richtwerte ermittelt. Deren Veränderung wird dann über die Zeit beobachtet und für Verhaltens-Tipps ausgewertet. Für den personenbezogenen Längsvergleich sind SDNN und RMSSD gleichermaßen geeignet, wenn auf standardisierte Messbedingungen geachtet wird (siehe Studie SDNN statt RMSSD).
Robustheit
Für die Praxis ist immer wichtig, wie empfindlich ein HRV-Wert für Messfehler und Anomalien ist. Die vom Sensor (EKG-Elektroden, Brustgurt, Ohr-Clip) und dem Datenerfassungsgerät gesammelten Messwerte beinhalten oft störende Anteile, die nicht zu einem typischen Herzschlag passen und zu sogenannten Artefakten im Ergebnis führen. Auf zwei solcher Störfaktoren möchte ich eingehen:
- Ungenauigkeit bei der Digitalisierung und
- Artefakte aufgrund von ungewöhnlichen Herzschlägen oder Bewegungen.
Um Ungenauigkeit bei der Digitalisierung zu veranschaulichen, soll eine HRV-Kurzzeitmessung herangezogen werden und deren RR-Intervalle gezielt verändert werden. Die Veränderungen sind so gewählt, dass sie Ungenauigkeiten bei der Messdatenerfassung simulieren (+/- 2 ms, zufällig verteilt). Die Auswirkung der Manipulation beobachten wir dann am errechneten SDNN-Wert.
Um den Einfluss der weiter oben erwähnten Artefakte zu veranschaulichen, nehmen wir wieder dieselbe HRV-Kurzzeitmessung und simulieren einen falsch ermittelten Herzschlag. Dabei wird eine R-Zacke simuliert, die im EKG-Signal circa 50 Prozent verfrüht detektiert wird. Das führt zu einem entsprechend kürzeren und einem längeren RR-Intervall, wie das folgende Diagramm zeigt. Die Auswirkung dieser Manipulation beobachten wir dann wieder am errechneten SDNN.
Bereits dieser Einfluss eines einzelnen verfälschten Herzschlags ist für eine verlässliche SDNN-Berechnung eigentlich nicht hinnehmbar. Mit diesem Beispiel wird aber auch deutlich, dass die SDNN weniger empfindlich für Artefakte ist als das Verfahren zur Berechnung des RMSSD.
Solche Artefakte kommen in der Praxis häufig vor. Vor allem bei Bewegung, insbesondere beim Sport und bei 24-Stunden-Messungen, treten sie meist wegen instabilem Hautkontakt der Mess-Sensoren auf. Eine weitere Ursache für Artefakte sind ungefährliche Extrasystolen (zusätzliche Herzschläge, die nicht von Sinusknoten erzeugt werden) oder gesundheitlich bedenkliche Rhythmusstörungen.
Um gewonnene RR-Intervalle trotz Artefakte für eine HRV-Analyse auswerten zu können, wird meist versucht, die Daten automatisch zu korrigieren. Dies gelingt in einfachen Fällen, wie im Beispiel eines einzelnen ungewöhnlichen Herzschlags, meist recht gut. Falls aber zum Beispiel wegen Kontaktunterbrechungen am Sensor stärker ausgeprägte Artefakte auftreten, sind die automatischen Verfahren auch schnell überfordert. Dann ist eine nachträgliche Bearbeitung der Messdaten von Hand das bessere Vorgehen. Solche manuellen Korrekturmöglichkeiten sind nach meinem Kenntnisstand nicht in Systemen für Endverbraucher vorgesehen, sondern eher für Wissenschaftler und Therapeuten. Besonders positiv aufgefallen ist mir die Korrekturmöglichkeit mit Hilfe des Poincaré-Diagramms, wie das beim BioSign HRV-Scanner umgesetzt ist.
Ich hoffe, meine Erläuterung der Berechnung des SDNN-Wertes ermöglicht auch HRV-Interessierten mit weniger technischer Vorbildung, eine Vorstellung der Zusammenhänge zu entwickeln.
P.S.: Die Beispieldaten wurden mit einem HRV-Scanner (Modell: Professional) des Herstellers BioSign gemessen, exportiert und mit Hilfe der Programmiersprache R von Erich Langenbuch aufbereitet.